Multiplication Order of Transformation Matrix

投稿日 |

TL;DR

  • Always be aware that whether your transformation is intrinsic or extrinsic.
  • Multiplication order of quaternions or transformation matrices is inverted between the two.

In this article, right-handed system is used.

Problem Definition

Let’s think of composite transformation $T_c$, which applies $T_1$ first, and then $T_2$.

  • $T_1$: Rotate 90 deg around x-axis
  • $T_2$: Rotate 180 deg around z-axis

Which is correct, $T_c = T_1 T_2$ or $T_c = T_2 T_1$ ?
Actually both can be true, we are missing something to identify $T_c$.

Extrinsic case

In extrinsic transformation, both $T_1$ and $T_2$ are described on the original coordinate.
Sometimes the original coordinate can be called world coordinate or fixed coordinate.

For example, let’s transform $P = (0, 0, 1)$ on the fixed frame.

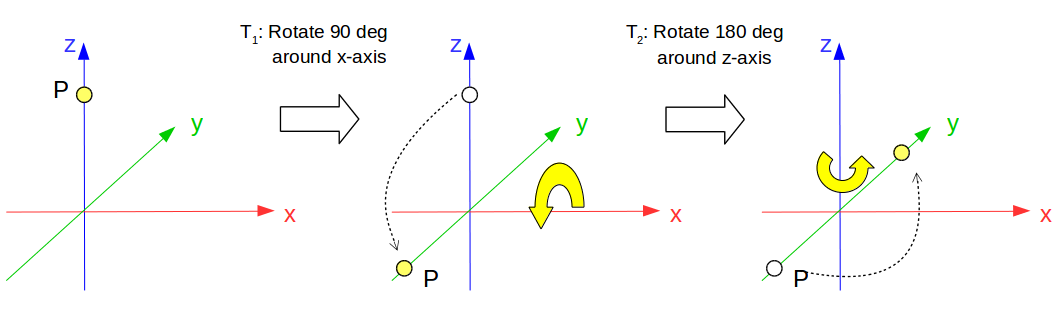
As you see, result should be $(0, 1, 0)$.

Intrinsic case

In intrinsic case, the transformation is not about point, but coordinate.
New coordinate emerges by $T_1$, and $T_2$ is described on the new one.

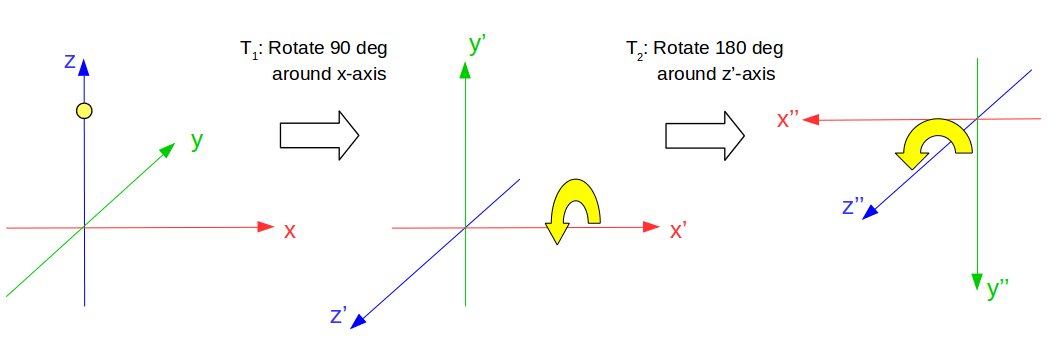
What’s important is $T_2$ is not about original z-axis, but new z’-axis.
With equation $P_{new} = T_c P$, where $P = (0, 0, 1)$, $P_{new} = (0, -1, 0)$,
because $(0,0,1)$ on x-y-z frame is $(0, -1, 0)$ on x’’-y’’-z’’ frame.

Multiplication Order

  • Extrinsic case: $T_c = T_2 T_1$
  • Intrinsic case: $T_c = T_1 T_2$

Let’s check by C++ code.
GitHub Link

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <iomanip>
#include <eigen3/Eigen/Dense>

#define _USE_MATH_DEFINES
#include <cmath>

int main(void) {
  using namespace Eigen;

  // Create transformation matrix
  // T_1 represents 90 deg rotation on x-axis
  // T_2 represents 180 deg rotation on z-axis
  Translation3f trans(0., 0., 0.);
  AngleAxisf rot1(M_PI_2, Vector3f::UnitX());
  AngleAxisf rot2(M_PI, Vector3f::UnitZ());

  Affine3f T1(trans * rot1);
  Affine3f T2(trans * rot2);

  Vector3f P(0., 0., 1.);

  // Extrinsic transformation
  Vector3f Pe = (T2 * T1) * P;

  // Intrinsic transformation
  Vector3f Pi = (T1 * T2) * P;

  // Show result
  std::cout << std::fixed;
  std::cout
    << "Extrinsic transformation: " << std::endl
    << Pe
    << std::endl
    << "Intrinsic transformation: " << std::endl
    << Pi
    << std::endl;

  return 0;
}

Results are the same as expected.

1
2
3
4
5
6
7
8
Extrinsic transformation: 
-0.000000
 1.000000
-0.000000
Intrinsic transformation: 
 0.000000
-1.000000
-0.000000