TL;DR
- Always be aware that whether your transformation is intrinsic or extrinsic.
- Multiplication order of quaternions or transformation matrices is inverted between the two.
In this article, right-handed system is used.
Problem Definition
Let’s think of composite transformation $T_c$, which applies $T_1$ first, and then $T_2$.
- $T_1$: Rotate 90 deg around x-axis
- $T_2$: Rotate 180 deg around z-axis
Which is correct, $T_c = T_1 T_2$ or $T_c = T_2 T_1$ ?
Actually both can be true, we are missing something to identify $T_c$.
Extrinsic case
In extrinsic transformation, both $T_1$ and $T_2$ are described on the original coordinate.
Sometimes the original coordinate can be called world coordinate or fixed coordinate.
For example, let’s transform $P = (0, 0, 1)$ on the fixed frame.
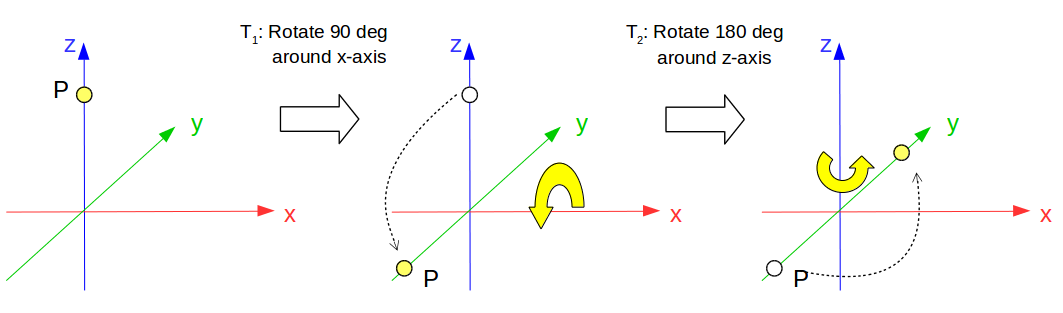
As you see, result should be $(0, 1, 0)$.
Intrinsic case
In intrinsic case, the transformation is not about point, but coordinate.
New coordinate emerges by $T_1$, and $T_2$ is described on the new one.
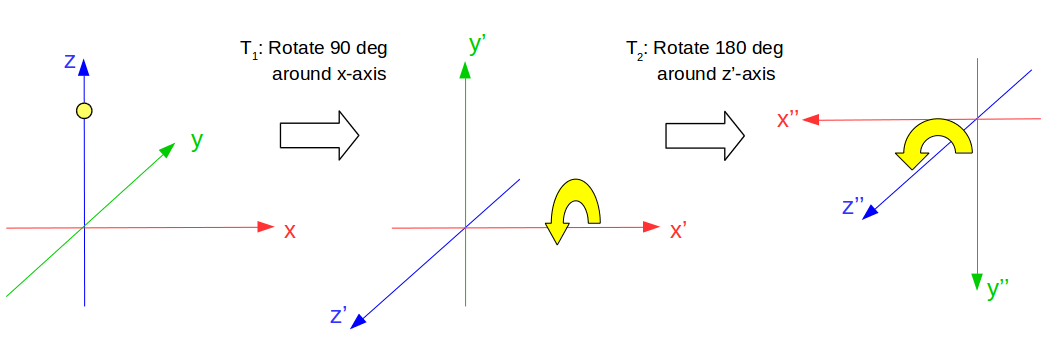
What’s important is $T_2$ is not about original z-axis, but new z’-axis.
With equation $P_{new} = T_c P$, where $P = (0, 0, 1)$, $P_{new} = (0, -1, 0)$,
because $(0,0,1)$ on x-y-z frame is $(0, -1, 0)$ on x’’-y’’-z’’ frame.
Multiplication Order
- Extrinsic case: $T_c = T_2 T_1$
- Intrinsic case: $T_c = T_1 T_2$
Let’s check by C++ code.
GitHub Link
1 |
|
Results are the same as expected.
1 | Extrinsic transformation: |